Table of Contents
Introduction
Methodology
Drawings
Sculptures
Discussion
Introduction
The Black Box Problem and Transparent Design
The black box problem is a term used in conjunction with discussions of artificial intelligence, detailing the inscrutability of machine learning algorithms. While these algorithms can be fed by curated data, the actual processes used by such models to arrive at an output are
uninterpretable. As Greg Lynn details in his 1999 book Animate Form, the advent of computer-aided design changed the way geometry is conceptualized in generating form in architecture. While these new design tools have pushed the boundary of design, they have also turned many designers into victims of a sort of black box problem. While I can drag a point in a digital space and observe its impacts on a curve, the algebraic transformations that the software executed to arrive there are obscured by layers of removal. My intent with this independent study was to employ a simple and explicitly detailed mathematical transformation to find forms from geometric objects. From here, I let the building process of model-making, detailed in the following pages, influence these constructions as well. I was hugely inspired by the works of Ron Resch, Goran Konjevod, and John Pickering, three artists/sculptors that used mathematical transformation or computer-based patterning to generate sculptures. There is an inherent beauty to math that many people never come into contact with through their experiences with it, and sculptors like these provide a novel and beautiful framing to what are otherwise mathematical constructions like any other that can be appreciated by a far wider audience.I sought not to complicate what I was researching and observing but instead to utterly simplify it. In the appendices, I include any specifics for those wishing to find them (the derivation of our transformation formula and tables of specific coordinates), but readers will notice that these details are largely omitted from the main body of this work. Perhaps, in this, I am creating my own black box for the reader, but I think it’s the kind that is present in any piece of artwork. There is always filtering —an inherent, interior process of transformation that frames and alters an individual work. If it seems interesting, please feel free to explore the appendices.Black Boxes as Discovery
The black box problem is not merely an obstacle; it is also a catalyst for critical inquiry and creative exploration. As the world around us adopts more and more implicit and ubiquitous uses of computational tools, an increasingly important tension arises between what we know and what we never will. How do designers balance leveraging the power of these tools while maintaining a clear understanding of their underlying logic? This study, rooted in mathematical transparency, aims to approach this issue through deliberate methodological choices.In my exploration, I found the act of maintaining transparency to be as much about process as it was about outcome. By consciously choosing not to rely on fully automated systems or algorithms during the form-finding stages, I engaged in a more direct dialogue with the transformations I was conducting. The simplicity of the chosen geometric objects—a cylinder and spheres—allowed me to observe the effects of each transformation without interference from extraneous variables. There were no questions about why an arc between three points looked the way it did. This simplicity was not a limitation; it was a framework for clarity. Each manipulation point of reflection, and a way to uncover potential hidden within basic mathematical relationships.As designers, we often confront the temptation to let sophisticated software dictate our creative decisions, even in ways we are completely unaware of. In doing so, we risk becoming passive participants in our own work. By emphasizing manual oversight and a hands-on approach, I aimed to resist this passivity. My process was an exploration of where control could be maintained and where chance or could be embraced.This transitional area between control and chance was particularly evident during the placement of the spheres that transformed the cylinder. While some placements followed structured patterns—symmetry, repetition, and reflection—others were guided by intuition and curiosity. These moments of intuition were crucial, introducing unpredictability and spontaneity into an otherwise rigorous process, and often forming the most exciting and beautiful moments of discovery. The black box became a threshold where the interplay between order and chaos could be observed and appreciated. The transition from digital form-finding to physical model-making further emphasized this balance. While the digital environment provided precision and flexibility, the physical models grounded the exploration in tactility. Material properties, scale, and spatial relationships offered insights that were not apparent solely in the numbers. By translating digital forms into physical objects, I engaged with a different kind of black box—the unpredictable nature of material behavior. This second black box, while different in origin, echoed the challenges of the first: an obscured process that required patience, experimentation, and a willingness to embrace uncertainty.Methodology
Mathematical Basis
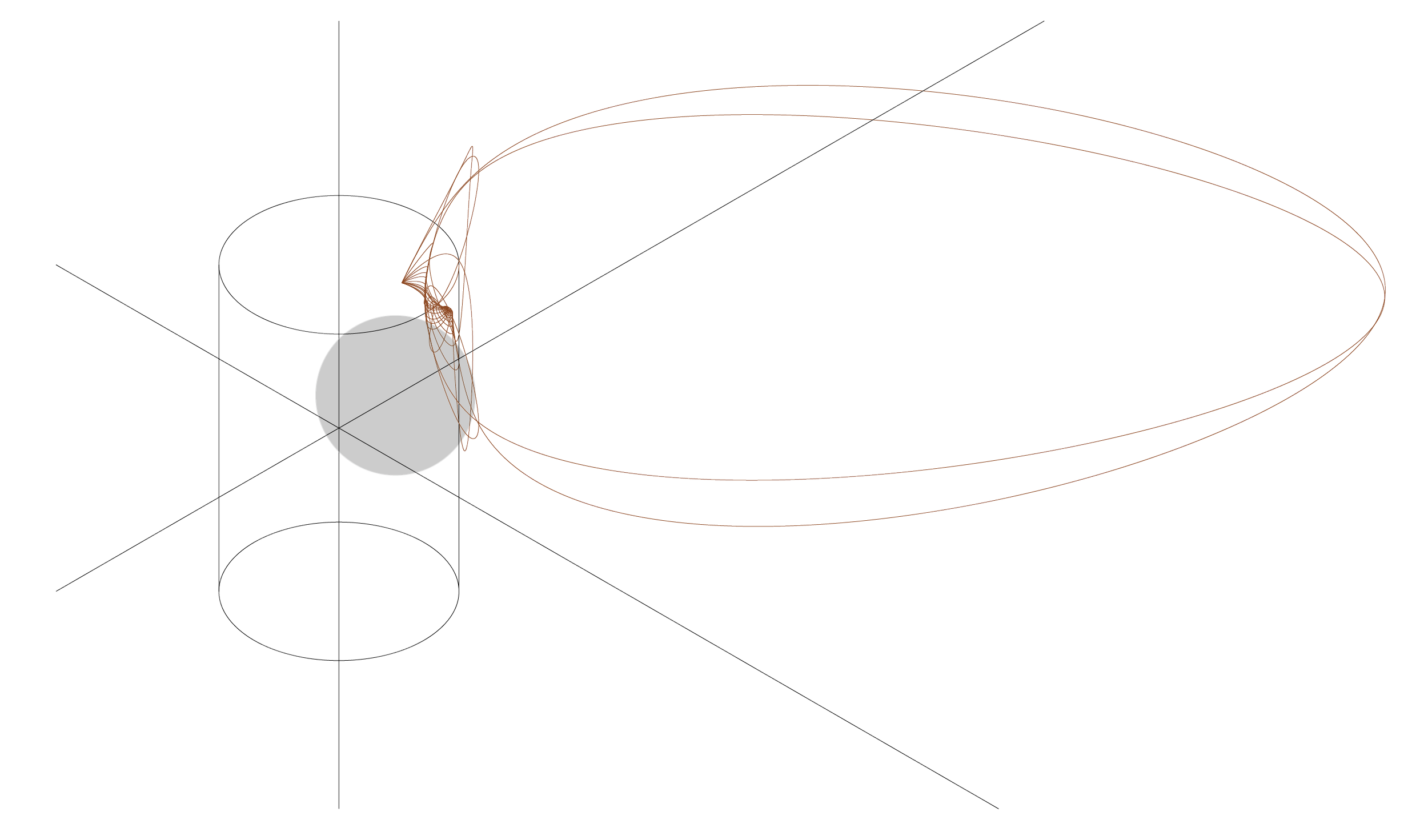
There were three particular parameters that I used to determine the mathematical transformation I would use as the basis to this explanation:Simplicity: The transformation used had to be simple enough that it could be explained relatively simply. While there are, for instance, many potentially applicable concepts in fields like topography and differential geometry, the point of this study was exploring the visual potentials of maintaining mathematical rigor in a way that could be easily explained and visualized to a non-mathematical audience. 2d and 3d applicability: The transformation had to be applicable in two and three dimensions, and specify the way that it would be applied to real numbers on the xy and xyz coordinate planes. I considered Mobius transformations as a candidate, which meet the two other criteria, but would require too much abstraction and interpretation to translate them to the real world because of their use of the complex plane. Graphability: While, as detailed by the criterion above, the input and output of the transformation had to be graphable, I specifically wanted the transformation itself to have a potential graphical representation. In this way, something like a Mobius transformation, which has a very helpful visual representation, fit this requirement perfectly, while something like projective transformations which had many other compelling benefits fails to be graphically interesting on its own.Through considerations of these parameters, I determined that spherical inversion (in three dimensions) was the transformation I would use for this project. Figure 1 shows the basic concept of inversion (in two dimensions), which moves a point from inside of a circle to its respective position outside or vice versa. To invert a point using geometric construction, which is wha the figure illustrates, first a ray is drawn from C, the center of the circle, to A and the continuing out from the circle. Then a perpendicular line to this ray is drawn, intersecting it at point A. Then a tangent line to the circle is drawn where the perpendicular line intersects the circle. Where this tangent line meets the ray from C to A is the location of A’, the inverted point. From here, the mathematical expression can be derived. This equation represents the definition of the inverse, where C is the center of the circle , r is the radius, and A is the point being inverted. After rearranging this expression and using the distance formula to find the lengths of CA and CA’ (see appendix), the the location of a point A(x,y,z) can be found by:Mathematical Basis
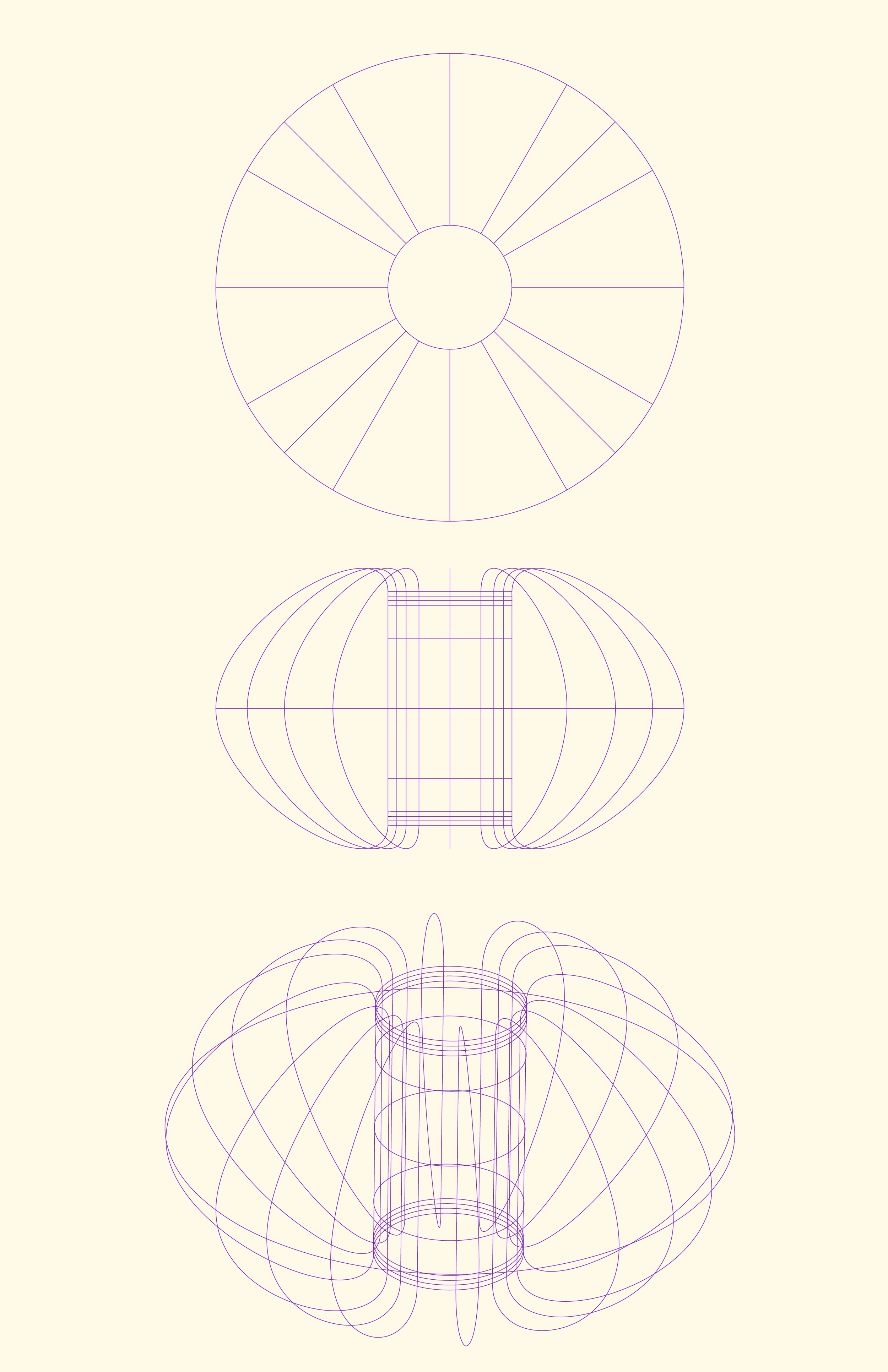
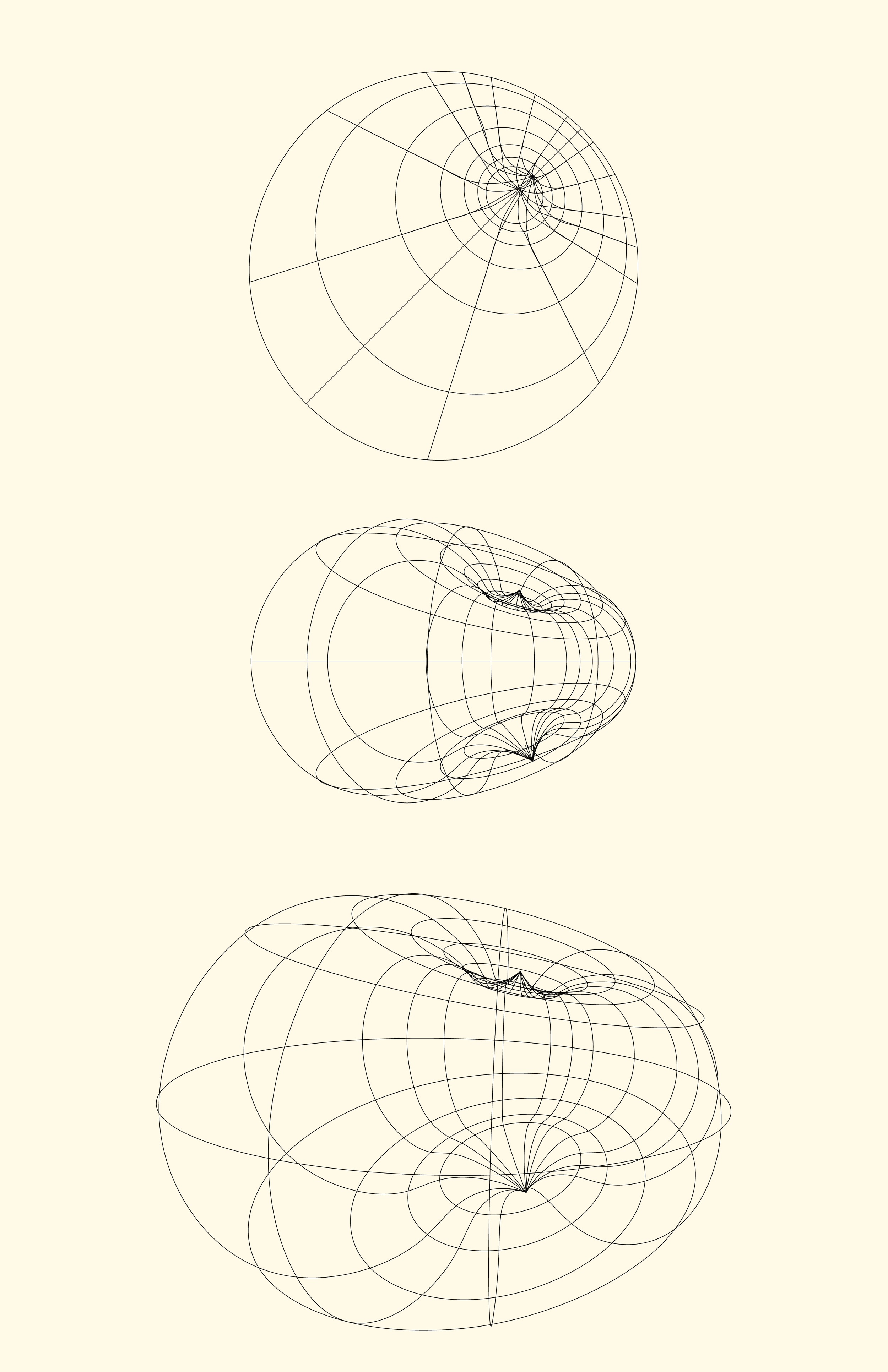
After establishing the mathematical basis for my exploration, I want to establish the actual methodology I will be using throughout. While I stated this will be done “by hand,” I want to clarify the meaning of that phrase with respect to this research.I did not manually calculate the rows and rows of values needed to carry out this transformation. Nor did I ever intend to take on graphing with a ruler and a pencil. “By hand” refers specifically to ensuring that mathematical transparency is maintained throughout this exploration. I use a calculator to compute tables of values, which are then graphed digitally in Rhino. Because I am working in three dimensions, Rhino’s 3D environment and ability to take in typed coordinates allows me to use it soleley as a graphing tool. This choice of tools also allows me to more easily move between the formal exploration and model making aspects of this study while maintaining the intended mathematical integrity.While even this involves a fair amount of tedium, the point of this is to allow to natural emergence of form without too much selection and filtering in the early stages. I intentionally never modeled these forms through three dimensional graphing or parametric modeling software because I didn’t want the process of engaging with natural form discovery to be itnerrupted. Even when transformations did not necessarily yield engaging forms that I wanted to continue with, I wanted the filtering to happen in a later part of the process than the initial form finding exploration.Additionally, to provide another limitation that narrowed the focus of this exploration, I decided that I would track variation by transforming only one object—the cylinder of radius 3 between z=5 and z=-5. I also decided to only transform it around spheres with a radius of 2. Ultimately, that meant that the only change would be where this sphere was placed. In deciding on locations to place this sphere, there were moments when I explored symmetry and pattern, moving the sphere at regular intervals or reflecting it across an axis, but also moments when I would just place it somewhere, wondering what would happen if I moved it far outside the cylinder, right at its border, etc.After the cylinder was transformed, I moved into the more organic, design oriented phase. I changed scales, orientations, and considered its spatial properties, as well as engaging with material. Specifically, I discovered throughout the process that I wanted to explore how transformation could be represented through model-making as well, utilizing not just the end product of a transformed shape, but other data that would otherwise be ignored.
When I got to the model making phase, I did use tools in Rhino that went beyond its graphing capabilities. However, in designing my models, I worked mostly in planes and flat surfaces that could be derived from the information I had collected instead of using more complex operations. I mostly used cutting and intersecting, which are things that would be possible if I was working with a pencil and paper. This was also a limiting factor when it came to the models, but allowed for a certain uniting character amongst the end products I designed.Drawings
Sculptures
This study model uses Objects 2 and 3 and their respective spheres of rotation.In wood are the objects, and in acrylic, to imply the fact that they are not actually present in the transformation but instead just a visualization of the center of inversion, are the spheres. Due to a scaling change in two dimensions, the objects and spheres are stretched, emphasizing the layers and the interactions between the different pieces of the transformation. More than either of the more finished models, it emphasizes this wound up, interactive aspect.Study Model No. 1
A model of a cut and enlarged section of Object 5.
This model turns it into topography, observing the changing contours. The use of cardboard shows the flowing lines and vertical connections through the aligned curved in corrugation.Study Model No. 2
Study model 3 is a study of Object 4 and study model 4 is a study of Object 1. These are simple layered models to observe the symmetry in what are the two most symmetrical Objects of the collection. Both are transformed based on spheres centered on the z-axis, with Object 1’s sphere centered on the origin.A duplicate of study model 3 is included in the first sculpture.Study Model No. 3 & 4
This sculpture models Object 4, the base cylinder, and its sphere.In clear acrylic, to suggest what was once there, is the cylinder, with holes to allow the sculpture to be hung and observed from below as well. In gray acrylic, less transparent but not opaque, is the sphere centered at (0, 0, -5) encasing the layer model of Object 4 in butterboard.The sculpture models the interaction between all three of these pieces, and allows for display both hung and placed on a surface, as to not lose any information that is encoded in the act of transformation.Sculpture No. 1
This sculpture models Object 5, the base cylinder, and its sphere.Like Sculpture No. 1, clear acrylic is used to model the cylinder. Unlike it, the scale of Object 5 allows for the sphere, simplified into intersecting wooden pieces, to function as a detail, providing an asymmetry reminiscent of this group of objects when they are on the coordinate plane.The base of the sculpture, for support, is made of wood, with a single wooden rib on which the paper ribs are supported. I wanted to use paper instead of a more controlled material like additional wood for the organic, natural flow and texture that it adds to the piece. Because of the bends in the paper, especially once they interact with glue, they fall closer and farther away from adjacent gills. I enjoyed the mushroom-gill-like interaction of these pieces in conjunction with the solid wood frame and sphere that appears to float.Sculpture No. 2
Discussion
This exploration into mathematical transformation and its sculptural outcomes revealed several key insights about the relationship between transparency, process, and creative discovery. Central to this study was the desire to balance the clarity of mathematical rigor with the unpredictable nature of artistic creation.Transparency and Creativity
One of the most significant takeaways was the importance of maintaining transparency in design processes. By deliberately avoiding fully automated algorithms and focusing on direct, traceable transformations, I was able to preserve an intimate understanding of each step in form generation. This transparency allowed me to see how even simple mathematical transformations could yield complex and unexpected results, reinforcing the notion that clarity does not limit creativity but rather enhances it.
The choice to work with basic geometric forms—a cylinder and spheres—provided a clear, manageable framework for transformation. This simplicity facilitated a deeper exploration of how small changes in parameters, such as the placement of the sphere, could lead to dramatic variations in form. By constraining the scope of the study, I could observe the nuances of each transformation without being overwhelmed by extraneous variables. Additionally, it served to prove that an algorithm or a singular process, especially one originating from basic geoemtric shapes, is absolutely not boring. Sometimes, the idea of exploring complexity seems the most engaging. I struggled at times with how basic of a transformation I had chosen, thinking that it felt silly and trivial. Participating in a creative process that revealed the distance between those two ideas, simplicity and triviality, was incredibly rewarding.Limitations and Challenges
However, these constraints also introduced significant limitations that impacted the study’s scope and outcomes. The decision to restrict transformations to a single type of object—a cylinder of radius 3 between z=5 and z=−5—limited the variety of potential forms. While this narrow focus allowed for clarity and depth, if I were to explore this, or a similar project further, I would want to include the exploration of different geometric shapes and their transformations. The forms generated were inherently constrained by the cylinder’s symmetry and regularity, which may have excluded more complex or irregular possibilities. The restriction of using spheres with a fixed radius of 2 for inversion further limited the diversity of transformations. Different radii could have yielded more varied and unexpected results, potentially revealing new patterns and forms. This fixed parameter, while ensuring consistency, may have prevented the discovery of richer or more nuanced geometries. I think, while these are both certainly limitations, they felt appropriate to the scope of this project.Another limitation was the methodology of manual oversight and transparency. While the intent was to avoid the black box effect by relying on traceable calculations and straightforward graphing in Rhino, this approach inherently limited the complexity of the transformations. More sophisticated operations, such as parametric modeling or algorithmic design, were intentionally avoided to maintain transparency. This choice, while philosophically aligned with the goals of the study, restricted the potential for exploring forms that might emerge from more complex computational processes. Similar to the previous limitation, this seemed slightly outside the scope of what I intended to accomplish, but a study of parametric modeling software that revealed insights allowing the user to rebalance the level of user control versus behind-the-curtain would be a useful extension of this study.Additionally, the reliance on cutting and intersecting operations in Rhino, chosen to maintain a connection to traditional design methods, constrained the complexity of the physical models. While this was an attempt to stick to the philosophical purpose of the exploration, perhaps carrying this out entirely on paper with simple graphing tools would have avoided this, allowing things like folding, bending, and pasting together that I kept out of the process because it meant too much reliance on software.Conclusion
Despite these limitations, the constraints also served as a framework for creative discovery. By narrowing the focus and restricting the tools and parameters, the study encouraged a deeper, more reflective engagement with each transformation. The limitations fostered a sense of discipline and intentionality, forcing me to explore the full potential of a simple transformation rather than being overwhelmed by endless possibilities.In this way, the restrictions were both a hindrance and a catalyst. They highlighted the tension between the desire for creative freedom and the need for methodological clarity. While the constraints may have excluded certain avenues of exploration, they also provided a clear structure that made the outcomes more coherent and focused.Ultimately, this project demonstrated that the black box, rather than being a barrier, can be a productive space for exploration. By choosing when to seek transparency and when to embrace ambiguity, designers can navigate the black box thoughtfully, using it as a tool rather than a hindrance. This study was not about solving my black box-adjacent problem but about engaging with it thoughtfully. By maintaining transparency where possible and embracing ambiguity where necessary, I sought to find a balance. The resulting forms and models are artifacts of a process that I attempted to detail throughout this paper. I hope for this approach to be a reminder of the value of clarity, intentionality, and the human touch. By shedding light on the processes behind the forms, we not only demystify the tools we use but also reclaim our agency as designers and creators. The black box may remain, but how we choose to interact with it can redefine its role in our work and our understanding of design.